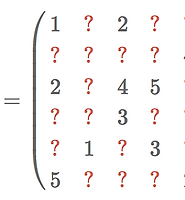| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 러스트
- 파이썬
- tcp
- 협업필터링
- 페이지랭크
- 파인만의 식당문제
- 인페인팅
- 비동기 프로그래밍
- react-cookie
- 자바스크립트 비동기
- 메세지인증코드
- recommender
- Readme image
- 커널제거
- 컴퓨터 보안 키분배
- 인공지능
- 키분배 알고리즘
- computer vision
- 딥러닝
- feynman's restaurant
- pagerank
- brew 권한
- Git
- 머신러닝
- rust
- 프라미스
- image restoration
- 커널생성
- cs231n
- Hits
- Today
- Total
Worth spreading
Matrix Factorization _ Part 1 본문
이 글은 Nicolas hug씨의
Understanding mtrix factorization
을 한글로 번역한 글입니다.
오역이나 잘못 설명된 부분을 발견하신 분은 댓글로 알려주시면 감사하겠습니다.
* rating은 점수, 점수를 주는 행위 두 가지 뜻으로 사용했으며 점수예측, rating prediction 등 단어를 섞어 썼으나 같은 뜻을 의미합니다.
* factorizing도 인수분해라는 어엿한 한국말이 있지만 그 느낌을 더 살기 위해 영문을 그대로 사용했습니다.
10여년 전, Netflix는 영화점수예측(predicting movie rating) 알고리즘 공모전 'Netflix prize'를 개최했다. 3년간 많은 연구진이 참여했고 그 중 matrix factorization은 효율적인 방법으로 과제를 해결해 큰 주목을 받았다.
이 글의 2 가지 목표
1. Matrix factorization이 어떻게 동작하는지에 대한 인사이트(insight)를 갖도록 하는 것. 이를 위해 PCA와 SVD가 어떻게 동작하는지 구체적인 예를 통해 소개할 것이다. 예제에선 User와 item이 latent factors vector space에서 벡터로 표현될 수 있으며 영화 점수가 두 벡터간의 dot product로 정의될 수 있다는 사실을 이용한다. 두 벡터간의 dot product로 정의된다는게 뭔가 와닿지 않는다면 이 글을 읽고 이해할 수 있길 바란다.
2. Matrix factorization 기반 predicting rating 알고리즘을 이해하고 구현하는 것
수학적인 부분은 최대한 간결하게 표현하려고 했다. 머신러닝 입문자를 대상으로 쓰여진 글이지만 전문가들에게도 충분히 좋은 글이 될 것이다.
4개의 파트로 이루어진 이 글은 파트1에서 우리가 풀고자 하는 문제를 정의하고 PCA에 대한 간략한 설명을 할 것이다. 파트2에선 SVD를 살펴보고 이것이 어떻게 점수와 연관되는지를 알아 볼 것이다. 파트3에선 SVD를 점수예측에 적용하는 방법에 대해서 살펴보고 matrix-factorization 기반 알고리즘을 수행하는 방법을 유도해 낼 것이다. 마지막 파트에선 파이썬의 surprise 라이브러리를 이용해 matrix factorization을 수행해 볼 것이다.
The problem
우리가 풀 문제는 점수예측(rating prediction)이다. 우리가 갖고 있는 데이터는 과거의 점수데이터이다.
[N x 5] 모양의 행렬로 행이 user, 열이 rating data인 sparse matrix다.
R에서 alice는 첫 번째 item에 1점을 준 것이고 charlie는 세 번째 item에 4점을 준 것이다.
우리 예제에선 item을 movie라고 가정하고 movie와 item 두 단어를 같은 뜻으로 사용할 것이다.
일반적으로 matrix R은 sparse matrix다.(99% 이상이 비어있다) 우리 목표는 점수가 없는 항목들(missing entries)을 예측해 채우는 것이다.
점수예측(Rating prediction) 기술은 여러가지가 있다. 우린 그 중에서 R을 factorize하는 방법을 사용할 것이다.
Matrix factorization은 SVD(Singular Value Decomposition)와 맞닿아 있다.
SVD는 선형대수의 매우 아름다운 한 대목이다!
만약 수학이 뭣같다는 사람이 있다면 SVD가 동작하는 모양세를 한번 소개해주자
이 글의 목표는 SVD가 rating prediction에서 어떻게 사용되는 지를 보여주는 것이다.
그런데 SVD에 대해서 알아보기 전에 PCA에 대해서 먼저 이해할 필요가
있다. PCA는 SVD에 비하면 조금 덜 아름답지만 그래도 충분히 아름답다.
A little bit of PCA
Recommendation problem은 잠시 옆으로 치워두고 Olivetti dataset을 가지고 PCA에 대해서 얘기해보자.
Olivetti dataset은 40명의 사람으로부터 추출한 400장의 그레이스케일 얼굴이미지 데이타셋이다. 다음은 데이터셋중 처음 10명의 사진이다.
좀 친숙하다..
무튼 각 이미지는 64x64이며 이 이미지들을 모두 한줄로 펴줄 것이다.(flatten)
이렇게 하면 길이 4096(64*64=4096)의 벡터 400개를 얻을 수 있다.
자 이제 우리 데이터셋을 400 x 4906 matrix로 표현해보자.
주성분 분석이라는 뜻의 PCA는 이 400명의 사람을 다음과 같이 표현했다.
이건 좀 소름끼친다..
우린 이 사진을들 주성분(principal components)이라고 부른다.
그리고 얼굴을 위와 같은 식으로 표현한 걸 eigenface라고 부른다.
Eigenface는 얼굴인식이나 optimizing yourtinder matches같은 문제에서도 잘 사용된다.
Eigenface라고 부르는 이유는 이것들이 X의 공분산 행렬의 eigenvector들이기 때문이다.
( 좀 더 자세한 사항은 여기를 참조)
기존 X가 400행을 가지고 있으니 (좀 더 명확하게 말하자면 X의 rank가 400이니) X는 400개의 주성분을 갖는다.
예상했듯이 각각의 주성분은 기존 얼굴들과 같은 차원의 벡터들이다.(4096)
우리는 이 녀석을들 creepy guys라고 부를 것이다.
자, 여기서 놀라운 사실 하나는 이 creepy guys가 orginal face들을 다시 생성해 낼 수 있다는 것이다.
다음 이미지들을 살펴보자 (10초분량의 gif파일이다.)









어떻게 이렇게 되는지 살펴보자.
400개의 original face들은 creepy guys들의 linear combination으로 표현될 수 있다.
예를 들어 우린 첫번째 original face를 첫 번째 creepy guy의 부분 + 두 번째 creepy guy의 부분 + 세 번째 creepy guy의 조금 ~ 마지막 creepy guy의 부분으로 표현할 수 있다.
다른 original face도 마찬가지이다.
모든 오리지널 페이스는 각 creepy guy들의 한 부분들로 표현될 수 있다.
이를 수학적으로 표현하면 다음과 같다.
여기서 creepy guy들을 가지고 놀고 싶은 사람은 여기서 해보자
Note: there is nothing really special about the fact that the creepy guys can express all the original faces. We could have randomly chosen 400 independent vectors of 64 x 64 = 4096 pixels and still be able to reconstruct any face. What makes the creepy guys from PCA special is a very important result about dimensionality reduction, which we will discuss in part 3.
Latent factors
우리가 creepy guy들한테 너무했던거 같다. 사실 그들은 creepy한 게 아니고 typical한 것이다.
PCA의 목표가 typical vector를 추출해 내는 것이다. 각각의
creepy/typical guy가 데이터에 숨겨진 특정한 면을 나타내는 것이다.
이상적인 세계에선 첫 번째 typical guy가 typical하게 나이가 많은 사람을 나타내고 두 번째 guy는 안경 쓴 사람들의 typical한 모습을,
이 외에도 웃는, 슬퍼보이는, 코가 큰 사람들을 나타낸다.
그리고 이 개념을 이용해 더 늙은지 어린지, 안경을 쓴 것 같은지 아닌지, 미소를 지은 것 같은지 아닌지 등을 정의할 수 있다.
하지만 현실에서 PCA가 보여주는 개념들은 그렇게 명로하지 않다.
Creepy/typical guy들과 연결되지 않는 불명확한 것들도 보이기 때문이다.
하지만 각각의 typical guy들이 데이터의 특정한 면을 나타낸다는 사실은 변하지 않는다.
우리는 PCA의 이러한 국면을 latent factors라고 부를 것이다
(latent, because they were there all the time, we just needed PCA to reveal them).
한마디로 말하자면, 우리는 각 주성분이 특정한 latent factor를 담고있다고 말할 수 있다.
좋다, 방금 얘기한 것들 모두 그렇다 치자.
근데 우리의 본 목적은 추천시스템을 위한 matrix factorization를 이해하는 것이다.
그래서 PCA가 추천시스템을 위해 뭘 한다는 거냐?
PCA는 plug-and-play method라고 할 수 있다.
즉 어떤 matrix에도 적용될 수 있다는 것이다.
만약 Matrix가 image를 표현한다면 위의 얼굴데이터와 같이 images의 PCA는 initial image들을 재구성해낼 수 있는 어떤 typical images를 나타낼 것이다.
감자(potato)를 표현하는 matrix가 있다면 PCA는 original 감자들을 구성해낼 수 있는typical 감자들을 나타낼 것이다.
그리고 만약 matrix가 점수를 포함한다면.. 이것이 우리가 풀 문제다.
PCA on a (dense) rating matrix
우선 시작하기 전에 dense한 rating matrix R이 있다고 생각해보자.
이 가상의 matrix R은 모든 유저들의 모둔 점수들을 가지고 있다.
물론 현실에선 이런 추천시스템은 없겠지만 그래도 한번 고려해보자.
PCA on the users
아까와 같이 row가 user고 column이 영화인 matrix R이 있다.
위에서 봤던 face matrix X와 유사하게 생겼다. 하지만 X의 row가 pixel value로 표현됐던 것과 달리 R은 user가 각 영화에 부여한 점수가 입력돼있다.
위 예제에서 PCA가 typical guys를 알려 준 것과 같이 이번엔 PCA가 어떤 typical raters를 나타내 줄 것이다.
다시 한번 말하지만 이상적인 세계에선 typical user와 관련된 개념은 명확한 뜻을 지닐 것이다.
예를 들어, typical user를 통해 a typical action movie fan, a typical romance move fan 등을 찾을 수 있을 것이다. 하지만 여긴 현실이다.
Typical user는 명료한 의미를 갖지 않을 것이다.
하지만 어느정도 근사할 수는 있다.
우리는 각 typical user가 어떨지 추정은 해 볼 수 있다.(이게 큰 의미를 갖지는 않는다. 단지 직관적인 의미를 전달하기 위한 것일 뿐)
이제 우리가 할 일은 다음과 같다.
각 user들(Alice, Bob..)은 다음과 같은 typical user들의 조합으로 표현될 수 있다.
예를 들어 Alice는 액션,코미디를 약간 좋아하지만 로맨스는 매우 좋아하는 사람이라고 생각해 볼 수 있다.
Bob의 경우는 Alice에 비해 액션을 좀 더 좋아하는 것으로 볼 수 있다.
PCA on the movies
그런데 우리 rating matrix를 transposed해보면 어떨까. 밑의 이미지와 같이 User가 아닌 영화를 row로 갖는 것이다.

이와 같은 경우 PCA는 typical face나 typical user가 아닌 typical movie를 나타낸다.
그리고 우린 이를 통해 각 typical movie의 어떤 특성과 연관지을 수 있다.
그리고 이 typical movie 또한 original movie를 다시 구성해 낼 수 있다.
여기까지 잘 따라왔다면 이제SVD에 대해 이야기 할 시간이다.
관련 글
- Understanding matrix factorization for recommendation (part4)
- Understanding matrix factorization for recommendation (part3)
- Understanding matrix factorization for recommendation (part2)
'ABCD > Data mining' 카테고리의 다른 글
| Basic Collaborative-Filtering (0) | 2018.07.21 |
|---|---|
| Feynman's restaurant problem (0) | 2018.06.26 |
| Pagerank(페이지랭크) (0) | 2018.06.16 |
| Matrix Factorization _ Part3 (0) | 2018.06.03 |
| Matrix Factorization _ Part 2 (0) | 2018.06.02 |